暴力解:merge 两个 array,取中位数,复杂度.
但这样的解法完全没有利用到这两个数组都是「有序」的这个信息。所以我们思考的时候,要考虑「有序」会给我们什么额外信息呢?
有序
这个中位数的特性就是,它一定能把 array 分成两部分,左边的都比它小,右边的都比它大。
A,B merge 后的 array, C, 的中位数,也能把这个 array 分成两部分。以下均假设 C 的长度是偶数(如果是奇数,一半的元素数量是floor(n/2) + 1,这一点在代码中有处理到)。如[1 2 3 4 5 6],那么它的一半的长度为 3。由于这个数组里的全部元素都来自 A 和 B,前半段里肯定有n1来自 A,n2来自 B。
如果我们知道n1,n2,能不能找到 C 的中位数呢?
设一半的长度为k,我们需要找到(C[k-1] + C[k])/2。
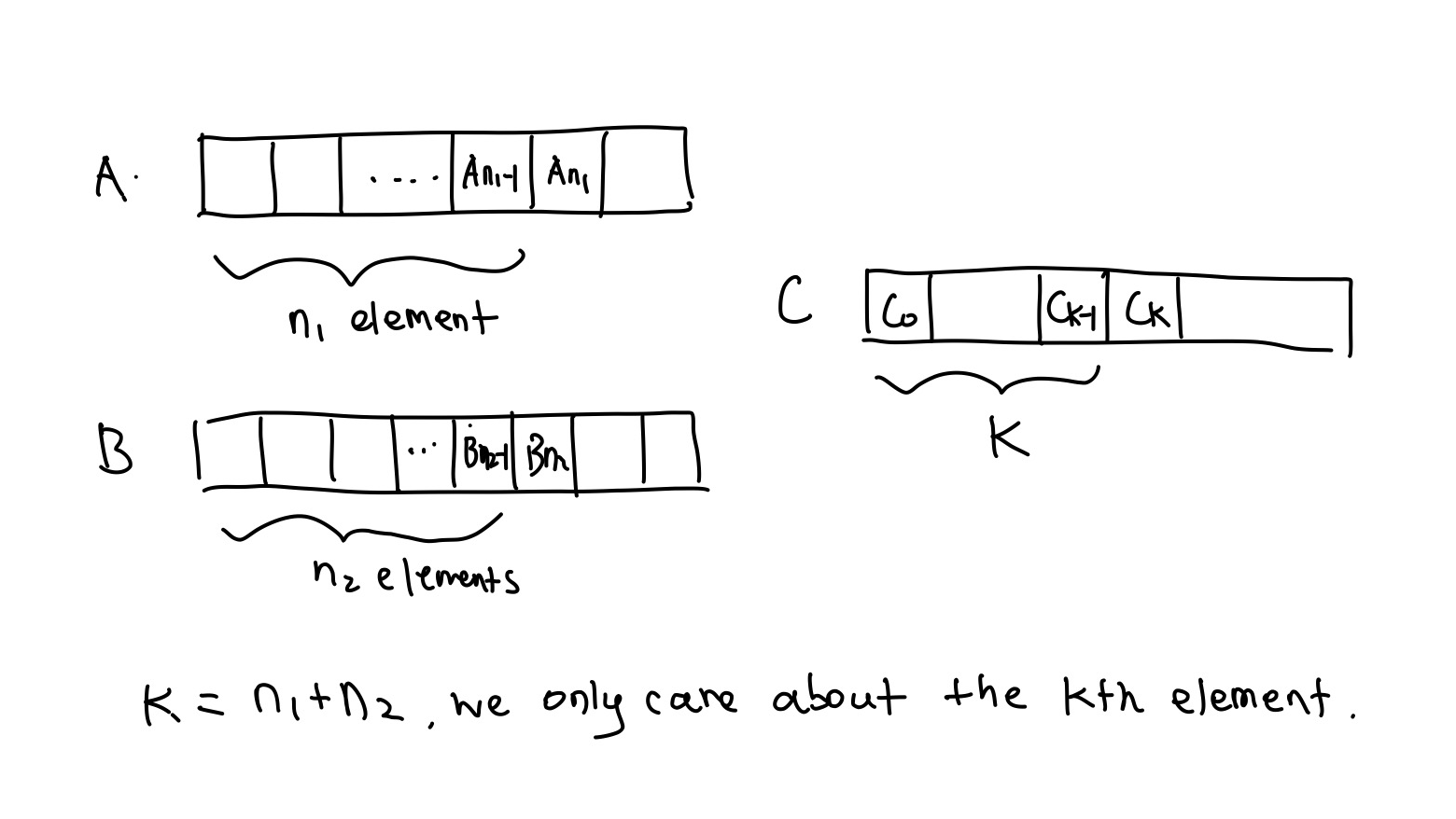
因为 A 和 B 有序,第 k 个数是前半段最大的。An1-1和Bn2-1分别是 A 和 B 里这部分最大的一个,那么只要找出他俩的max,这个数一定是前半段最大。同理,第k+1个数肯定来自于An1和Bn2,他们要争夺「后半段最小」这个位置。
所以,如果知道n1和n2,我们就能求到 C 的中位数。
怎么求 n1 和 n2
首先,k 是已知的,k=(len(A)+len(B))//2。如果知道了 n1,可以通过 n2 = k - n1 求到 n2。所以最终的问题是:如何找到 n1?
我们可以理解为,我们把 A 切了一刀,分成两部分。由于 k 是固定的,我们也能知道 B 在哪里被切了一刀
随便切一刀
L1 R1
A = a0 a1 a2 | a3 ... am
L2 R2
B = b0 b1 b2 b3 | b4 ... bn随便切一刀
L1 R1
A = a0 a1 a2 | a3 ... am
L2 R2
B = b0 b1 b2 b3 | b4 ... bn这一刀左边属于 C 的前半部分,所以必然有。所以,如果这一刀切的位置是正确的,这两个条件一定成立。如果不成立,我们便可以排除掉一些元素。
如何排除元素
这种情况下,我们需要更小的 L1,才有可能让它比 R2 小,那么这一刀得往左移,因为右边的都比 L1 大,绝对不可能小于 R2。
我们需要更大的 R1,所以这一刀得往右移。
移动多少呢?
我们自然是可以一个一个地移,但要知道,我们的目的是「尽快」找到一个 ,从而使成立。这里要再次利用「有序」这个特点,引入 binary search。
就好像猜数字那个例子,每一次我会告诉你,你的猜测是比我想的数大还是小,你自然可以一个一个地逼近我的答案。假设这个数在 0 到 100 之间,如果我想的是 78,你猜的 1,如果你按照 1, 2, 3, …这个顺序来猜,再猜 77 次,可以猜对。但如果你用二分法,下一个你猜 50,直接就排除掉了一半的元素。
这里也是一样,
看看下一刀可以切哪里
? ? L1 R1
A = a0 a1 a2 | a3 ... am
L2 R2
B = b0 b1 b2 b3 | b4 ... bn看看下一刀可以切哪里
? ? L1 R1
A = a0 a1 a2 | a3 ... am
L2 R2
B = b0 b1 b2 b3 | b4 ... bn我们可以确认新的 L1 来自区间[0, L1-1],那么我们先猜这个区间的中位数,如果还是太大,那整个[mid, L1-1]区间都可以被排除掉。这样肯定比一次挪一个有效率。
边界情况
实现中,我们的 cut 为 R,L 为 R-1。当 cut 为 0 时,cut-1 是不存在的。
先思考,如果正确的 cut 在 a0,那么 C 的前 k 个元素里,没有任何来自 a。那意思就是,a0 大于等于b0, b1 ... bk-1。由于是最大的一个,只需要确定是否成立,即。在这个比较中,我们并不需要。为了让边界一般化,不比较,等同于这个条件 always true,这样对后来的比较不会造成任何影响。那么,就能保证它小于等于任何 R2。同理,当我们想无视时,只需要。
代码和几个细节
def findMedianSortedArrays(nums1, nums2):
n1 = len(nums1)
n2 = len(nums2)
# make sure we're searching in the shorter one
if n1 > n2: #[1]
return self.findMedianSortedArrays(nums2, nums1)
# If there's nothing in nums1, just return median of nums2
if not n1: return (nums2[(n2 - 1) // 2] + nums2[(n2) // 2]) / 2
k = (n1 + n2 + 1) // 2
cutL, cutR = 0, n1 #[2]
cut1 = 0
while (cutL <= cutR):
cut1 = cutL + (cutR - cutL) // 2
cut2 = k - cut1
L1 = nums1[cut1 - 1] if cut1 > 0 else float('-inf')
R1 = nums1[cut1] if cut1 < n1 else float('inf')
L2 = nums2[cut2 - 1] if cut2 > 0 else float('-inf')
R2 = nums2[cut2] if cut2 < n2 else float('inf')
if L1 > R2: # need smaller L1, move left
cutR = cut1 - 1
# [3]
elif L2 > R1: # need larger R1, move right
cutL = cut1 + 1
else: # right cut
size = n1 + n2
if size % 2 == 0: # even
return (max(L1, L2) + min(R1, R2)) / 2
else:
return max(L1, L2)
return -1def findMedianSortedArrays(nums1, nums2):
n1 = len(nums1)
n2 = len(nums2)
# make sure we're searching in the shorter one
if n1 > n2: #[1]
return self.findMedianSortedArrays(nums2, nums1)
# If there's nothing in nums1, just return median of nums2
if not n1: return (nums2[(n2 - 1) // 2] + nums2[(n2) // 2]) / 2
k = (n1 + n2 + 1) // 2
cutL, cutR = 0, n1 #[2]
cut1 = 0
while (cutL <= cutR):
cut1 = cutL + (cutR - cutL) // 2
cut2 = k - cut1
L1 = nums1[cut1 - 1] if cut1 > 0 else float('-inf')
R1 = nums1[cut1] if cut1 < n1 else float('inf')
L2 = nums2[cut2 - 1] if cut2 > 0 else float('-inf')
R2 = nums2[cut2] if cut2 < n2 else float('inf')
if L1 > R2: # need smaller L1, move left
cutR = cut1 - 1
# [3]
elif L2 > R1: # need larger R1, move right
cutL = cut1 + 1
else: # right cut
size = n1 + n2
if size % 2 == 0: # even
return (max(L1, L2) + min(R1, R2)) / 2
else:
return max(L1, L2)
return -1-
为什么一定要在短的那个里搜索?
我们需要保证
k-cut1是一个非负数,因为最少也就是有零个元素来自某个数组。。但如果我们不选择短的那个,cut1 就有可能大于 k。那为什么短的那个不可能出现
cut1 > k?我们限制了, 如果,那么。如果 C 的长度是偶数,k 正好是一半的元素,这个自相矛盾;如果是奇数,k 为一半的元素加一,比一半的元素还多,2k 更是超过了 C 的长度,矛盾。
-
cutR为什么可以是n1,不是超过数组长度了么?首先要明确 cutR 代表了什么。cutL 和 cutR 代表了这个 cut 可能出现的区间。如果 cut 在 n1 这个位置,证明 A 里面的全部元素都在前半段,也就是 A 的 max 小于 B 的 min。这里我们在边界条件已经处理过了。
-
这里的
elif可以是if么?能不能再多排除一点?假设这两个条件同时成立,,那么与矛盾,所以是不可能的。