This part focuses on the idea behind the solution. The actual implementation will be covered in Part2.
Problem
Given an unsorted array of integers, find the length of longest increasing subsequence. Example from LeetCode:
Input: [10,9,2,5,3,7,101,18]
Output: 4
Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4.Input: [10,9,2,5,3,7,101,18]
Output: 4
Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4.The dynamic programming solution is quite straightforward. But I’m surprised to see the relationship between the card game Patience and LIS.
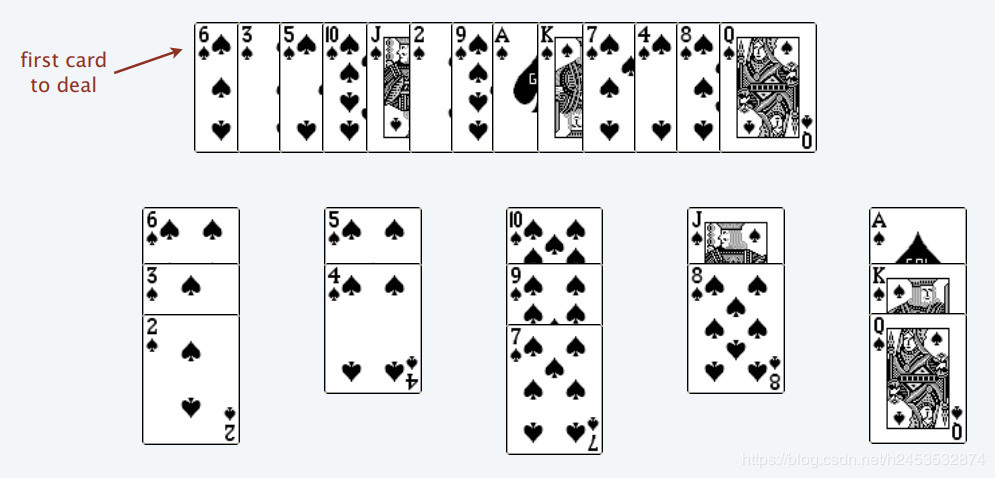
Princeton slides
Patience
Rules
-
You can only place a lowered-valued(or equal-valued) card on top of a higher-valued card, e.g.,
2on top of3. Note Ace is NOT1here. -
You can form a new pile and put your card onto it.
To understand why it’s related to LIS, we need to make two observations.
Observation1
For any legal strategy, length of any increasing subsequence
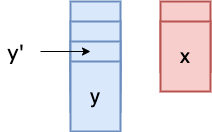
Claim: Any increasing subsequence can use at most one card from each pile.
Proof
Assume we used and from this pile. Since is on top of , .
If , they can’t form an increasing sequence. “increasing” is different from “non-decreasing”.
If , the only way to use both cards in an increasing sequence is to place after in that sequence. But is on top of , so comes before in the original array.
For example, [y', y] = [5, 2], 5 -> 2 is not an IS.
Thus, you can’t form an IS with more than one card from a pile length of any IS is at most .
Greedy algorithm
Idea: put the new card on the leftmost pile possible, i.e., the first pile from left to right, such that .
If we play the game with this strategy, we will notice that top cards form an IS(increasing sequence). For example,
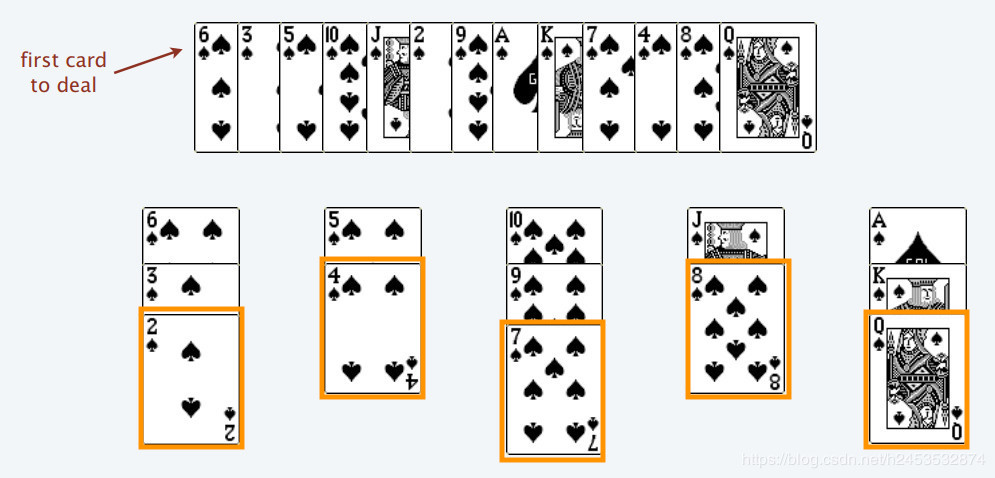
2 4 7 8 Q is an IS.
Let’s prove this.
Observation2
Using the greedy strategy, top cards of piles increase from left to right at any time of the game
Proof

Assume , so we don’t have an IS. We have two cases:
-
comes before
Then must be placed on top of by the algorithm. Contradiction.
-
comes after
Since is put into the red pile, or it’ll be in the blue pile by our greedy algorithm. is on top of , so . But we assumed , so which contradicts .
With these two observations, we can go head and prove the duality.
Duality
Lenght of LIS = #piles using the greedy strategy
Let the length of LIS be , and be the created by the greedy algorithm. For an inequality, we have to show and directions.
This follows directly from length of nay IS in observation 1. LIS is an IS, so .
From observation 2, we know top cards of piles increase from left to right at any time of the game using this algorithm.
Note that the top cards are in general not an increasing subsequence — Berkeley notes
In this case, the top cards are 2 4 7 8 Q, but 4 comes after 7 in the original deck, so 4 -> 7 is not an IS.
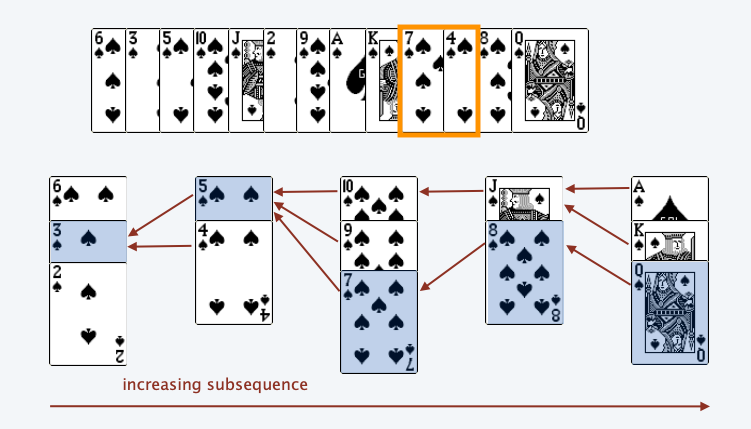
To keep track of a valid IS, at the time of insertion of a card , we keep a pointer from to the current top card to the left of . For example, when 5 is inserted, 3 is the top card on its left, so there’s an arrow from 5 to 3.
Assume , let the top card on the pile be . Since we have piles, we can follow the pointers starting at to get . Note that from left to right, . Thus, we get an IS of length .
But we claimed the length of the longest IS is . contraditcts that, so